Can’t-Miss Takeaways Of Tips About How To Learn Significant Figures

Look at the next digit to the right. In the bbc bitesize ks23 maths guide, you can learn how to round numbers to three significant figures. Each number has two significant figures therefore the answer can have a maximum of two significant figures.

how to make money in vending how to get out of a rogers cell phone contract how to lose weight step by step how to make money on second life how to get over cold faster how to get rid of razor bumps on head how to keep a worm farm how to get a free guardian on adventure quest

How Many Significant Figures Should You Use?

Significant Figures

Significant Figures Learn Important Rules Of Mathematics Embibe

Rounding Numbers (significant Figures) Bbc Bitesize

11p02 Units And Measurement Significant Figures ,

Significant Figures Chemistry Video Clutch Prep

Identify the number of significant digits/figures in the following given numbers.

How to learn significant figures. Significant figures are the number of digits in a value, often a measurement, that contribute to the degree of accuracy of the value. Learn how to find significant figures in a few minutes. Is it 5 or more?

Multiply or divide the numbers in the problem as you would normally. Calculate the number of significant figures for an assortment of numbers. The blended learning approach combining online teaching and virtual reality technology plays a positive role in students’ learning and is useful and effective in dental education.

Enter a number or expression. You'll also learn what a significant number is! Once we have started counting significant figures, we continue to count all digits including any zeros.

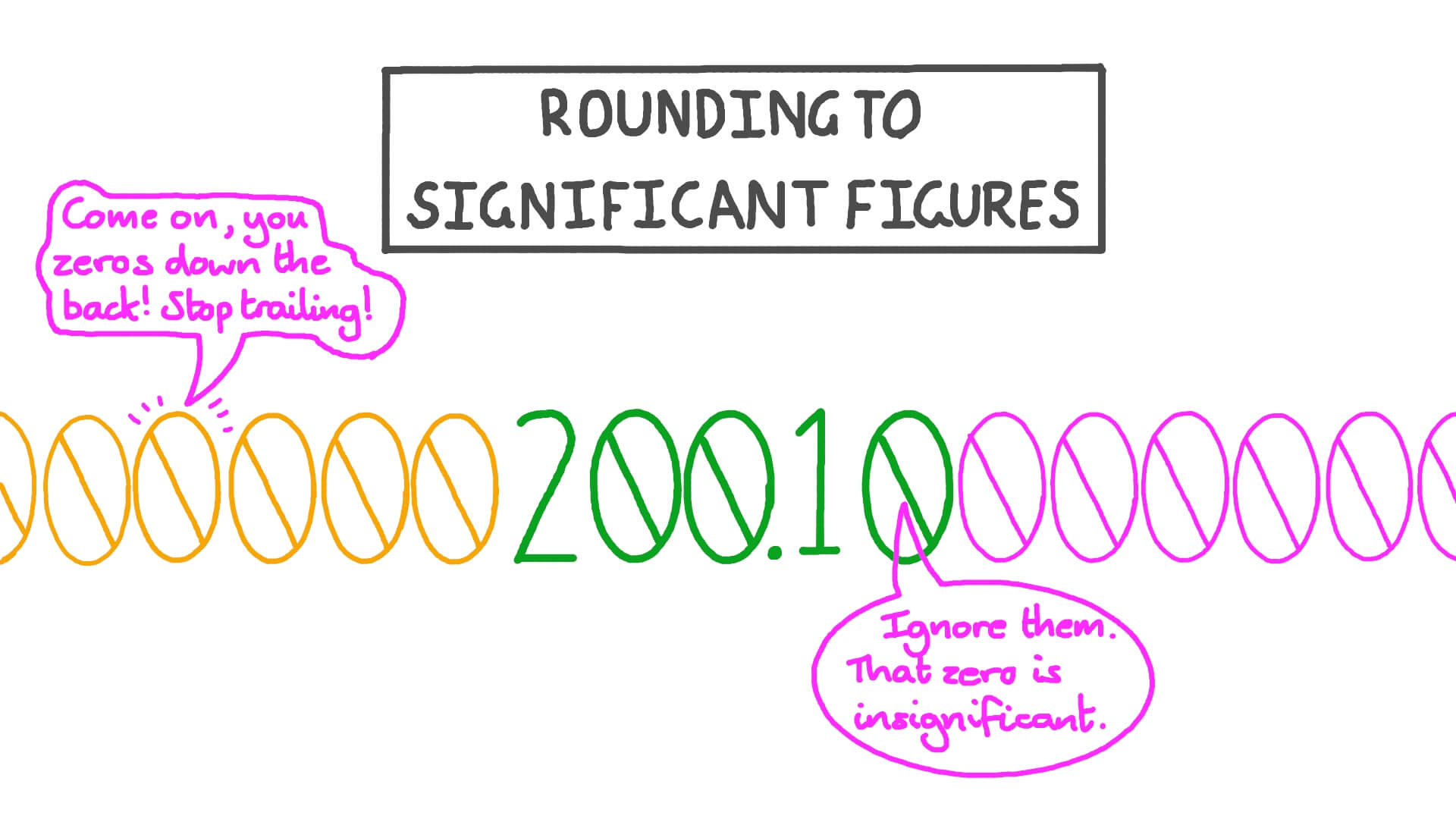
You simply include all the significant figures in the leading number. How to identify significant figures in order to identify significant figures: Rules for significant figures rounding significant figures.

Apply the concept of significant figures to limit a measurement to the proper number of digits. A) multiply 3.1 by 3.5. Well, i suspect it is not exactly 29,029 feet tall.

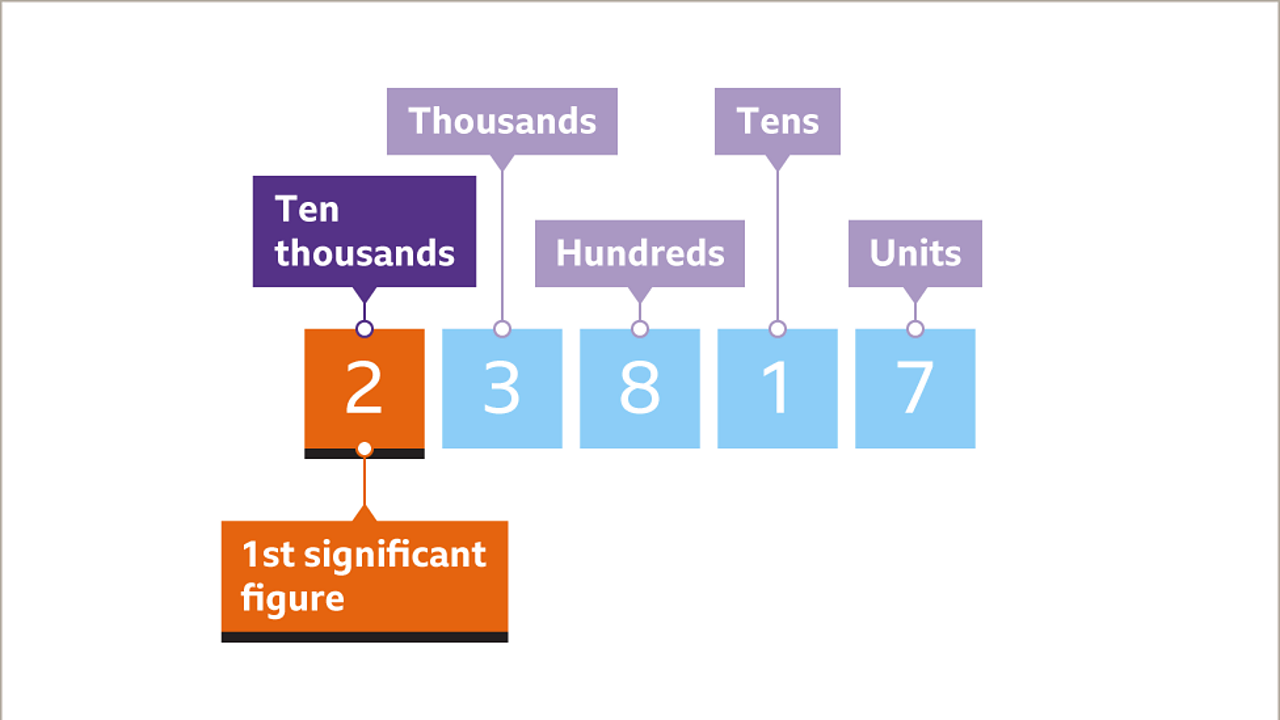
Label the number of significant figures. Locate the significant figure for the degree of accuracy required. The 2 is the 3rd significant figure.

This video helps you understand how to use all the significant figure rules, and how to round to the right number of sig figs when. The 5 is the 5th significant figure. A number is rounded off to the required number of significant digits by leaving one or.

1 is the first significant figure of 0.10205. Significant figures are used to report a value, measured or. 3.1 x 3.5 = 10.85.

Significant figures, any of the digits of a number beginning with the digit farthest to the left that is not zero and ending with the last digit farthest to the right that is either not zero or that is a zero but is considered to be exact. If the number immediately to the right of the last significant digit is less than 5, it is dropped and the value of the last significant digit remains the same. So in this case the correct answer is 11.

M^{2} \ldotp$$but because the radius has only two significant figures, it limits the calculated quantity to two significant figures, or $$a = 4.5\; Recognize the number of significant figures in a given quantity. For example, in the number 0.004205, the '4' is the most significant figure.